Vì ô mã hỗ trợ cú pháp Python đầy đủ nên bạn có thể sử dụng nhận xét Python trong cửa sổ mã để mô tả mã của mình. Tuy nhiên, đôi khi bạn cần nhiều hơn một nhận xét dựa trên văn bản đơn giản để minh họa các thuật toán ML. ML sử dụng nhiều toán học và để giải thích các thuật ngữ và phương trình đó cho người đọc, bạn cần một trình soạn thảo hỗ trợ LaTex – một ngôn ngữ để biểu diễn toán học. Colab cung cấp Ô văn bản cho mục đích này.
Một ô văn bản chứa một số phương trình toán học thường được sử dụng trong ML được hiển thị trong ảnh chụp màn hình bên dưới –

Khi tiếp tục chương này, chúng ta sẽ thấy đoạn mã để tạo ra kết quả trên.
Ô văn bản được định dạng bằng cách sử dụng markdown – một ngôn ngữ đánh dấu đơn giản. Bây giờ chúng ta hãy xem cách thêm ô văn bản vào sổ ghi chép của bạn và thêm vào đó một số văn bản chứa các phương trình toán học.
Ví dụ về đánh dấu
Chúng ta hãy xem xét một số ví dụ về cú pháp ngôn ngữ đánh dấu để chứng minh khả năng của nó.
Nhập văn bản sau vào ô Văn bản. This is **bold**.This is *italic*.This is ~strikethrough~.Đầu ra của các lệnh trên được hiển thị ở phía bên phải của Ô như được hiển thị ở đây.

phương trình toán học
Thêm một ô văn bản vào sổ ghi chép của bạn và nhập cú pháp đánh dấu sau vào cửa sổ văn bản – $\sqrt{3x-1}+(1+x)^2$Bạn sẽ thấy mã đánh dấu hiển thị ngay lập tức ở bảng điều khiển bên phải của ô văn bản. Điều này được hiển thị trong ảnh chụp màn hình bên dưới

Nhấn Enter và mã đánh dấu biến mất khỏi ô văn bản và chỉ hiển thị kết quả đầu ra được hiển thị.
Chúng ta hãy thử một phương trình phức tạp hơn như được hiển thị ở đây – $e^x = \sum_{i = 0}^\infty \frac{1}{i!}x^i$
Kết quả đầu ra được hiển thị ở đây để bạn tham khảo nhanh.

Đây là mã cho các phương trình mẫu được hiển thị trong ảnh chụp màn hình trước đó
Constraints are
- $3x_1 + 6x_2 + x_3 =< 28$
- $7x_1 + 3x_2 + 2x_3 =< 37$
- $4x_1 + 5x_2 + 2x_3 =< 19$
- $x_1,x_2,x_3 >=0 $
The trial vector is calculated as follows:
- $u_i(t) = x_i(t) + \beta(\hat{x}(t) − x_i(t)) + \beta \sum_{k = 1}^{n_v}(x_{i1,k}(t) − x_{i2,k}(t))$
$f(x_1, x_2) = 20 + e - 20exp(-0.2 \sqrt {\frac {1}{n} (x_1^2 + x_2^2)}) - exp (\frac {1}{n}(cos(2\pi x_1) + cos(2\pi x_2))$
$x ∈ [-5, 5]$
>$A_{m,n} =
\begin{pmatrix}
a_{1,1} > a_{1,2} > \cdots > a_{1,n} \\
a_{2,1} > a_{2,2} > \cdots > a_{2,n} \\
\vdots > \vdots > \ddots > \vdots \\
a_{m,1} > a_{m,2} > \cdots > a_{m,n}
\end{pmatrix}$
Việc mô tả cú pháp đánh dấu đầy đủ nằm ngoài phạm vi của hướng dẫn này. Trong chương tiếp theo, chúng ta sẽ xem cách lưu tác phẩm của bạn.
Google Colab – Tiết kiệm công việc của bạn
Colab cho phép bạn lưu tác phẩm của mình vào Google Drive hoặc thậm chí trực tiếp vào kho lưu trữ GitHub.
Đang lưu vào Google Drive
Colab cho phép bạn lưu công việc của mình vào Google Drive. Để lưu sổ ghi chép của bạn, hãy chọn các tùy chọn menu sau – File / Save a copy in Drive…Bạn sẽ thấy màn hình sau
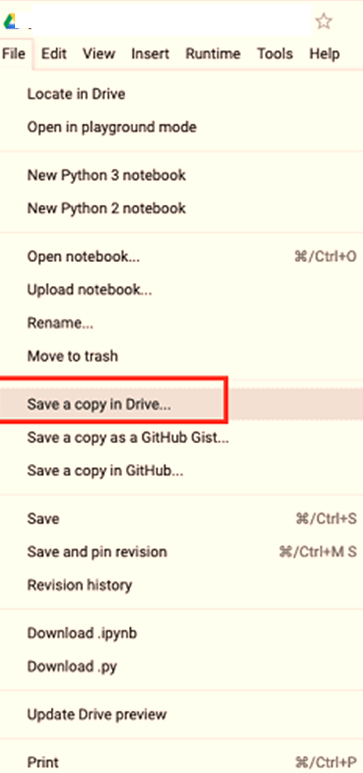
Hành động này sẽ tạo một bản sao sổ ghi chép của bạn và lưu nó vào ổ đĩa của bạn. Sau này bạn có thể đổi tên bản sao theo tên bạn chọn.
Lưu vào GitHub
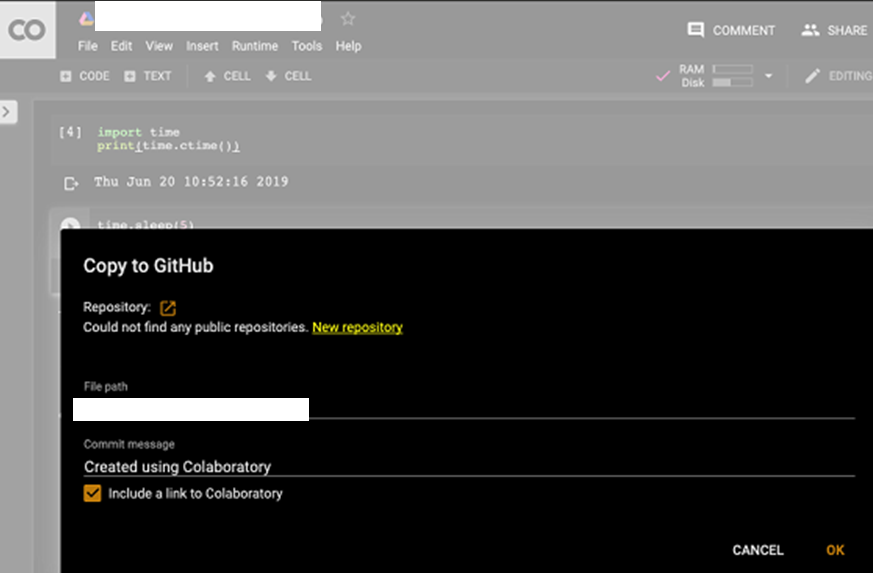
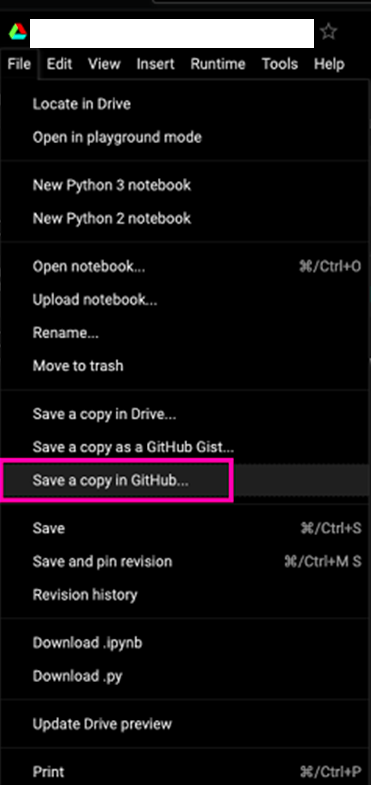
Bạn cũng có thể lưu tác phẩm của mình vào kho lưu trữ GitHub bằng cách chọn các tùy chọn menu sau – File / Save a copy in GitHub…Lựa chọn menu được hiển thị trong ảnh chụp màn hình sau để bạn tham khảo nhanh
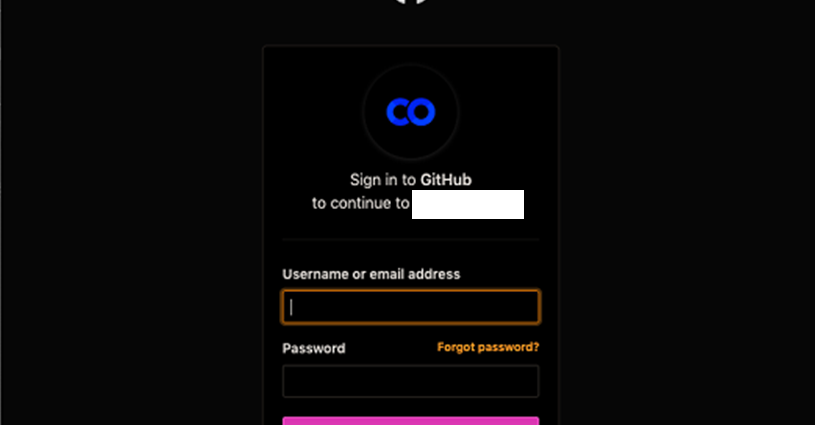
Bạn sẽ phải đợi cho đến khi nhìn thấy màn hình đăng nhập vào GitHub.
Bây giờ, hãy nhập thông tin đăng nhập của bạn. Nếu bạn không có kho lưu trữ, hãy tạo một kho lưu trữ mới và lưu dự án của bạn như trong ảnh chụp màn hình bên dưới