CNTK - Mô hình hồi quy logistic

Khái niệm cơ bản về mô hình hồi quy logistic

Hồi quy logistic, một trong những kỹ thuật ML đơn giản nhất, là một kỹ thuật đặc biệt để phân loại nhị phân. Nói cách khác, để tạo mô hình dự đoán trong các tình huống trong đó giá trị của biến cần dự đoán có thể chỉ là một trong hai giá trị phân loại. Một trong những ví dụ đơn giản nhất của Hồi quy logistic là dự đoán một người là nam hay nữ, dựa trên tuổi, giọng nói, kiểu tóc, v.v.

Ví dụ

Hãy hiểu khái niệm hồi quy logistic về mặt toán học với sự trợ giúp của một ví dụ khác –

Giả sử chúng ta muốn dự đoán mức độ xứng đáng về mặt tín dụng của một đơn xin vay tiền; 0 có nghĩa là từ chối và 1 có nghĩa là chấp thuận, dựa trên nợ , thu nhập và xếp hạng tín dụng< của người nộp đơn a i=4>. Chúng tôi thể hiện khoản nợ bằng X1, thu nhập bằng X2 và xếp hạng tín dụng bằng X3.

Trong Hồi quy logistic, chúng tôi xác định giá trị trọng số, được biểu thị bằng w, cho mọi tính năng và một giá trị sai lệch duy nhất, được biểu thị bằng .b Bây giờ giả sử,

X1 = 3.0
X2 = -2.0
X3 = 1.0

Và giả sử chúng ta xác định trọng số và độ lệch như sau –

W1 = 0.65, W2 = 1.75, W3 = 2.05 and b = 0.33

Bây giờ, để dự đoán lớp, chúng ta cần áp dụng công thức sau –

Z = (X1*W1)+(X2*W2)+(X3+W3)+b
i.e. Z = (3.0)*(0.65) + (-2.0)*(1.75) + (1.0)*(2.05) + 0.33
= 0.83

Tiếp theo, chúng ta cần tính P = 1.0/(1.0 + exp(-Z)). Ở đây, hàm exp() là số Euler. P = 1.0/(1.0 + exp(-0.83)= 0.6963

Giá trị P có thể được hiểu là xác suất của lớp đó là 1. Nếu P < 0,5, dự đoán là lớp = 0, ngược lại dự đoán (P >= 0,5) là lớp = 1.

Để xác định các giá trị trọng số và độ lệch, chúng ta phải có được một tập dữ liệu huấn luyện có các giá trị dự đoán đầu vào đã biết và các giá trị nhãn lớp chính xác đã biết. Sau đó, chúng ta có thể sử dụng một thuật toán, thường là Độ dốc giảm dần, để tìm các giá trị trọng số và độ lệch.

Ví dụ triển khai mô hình LR

Đối với mô hình LR này, chúng tôi sẽ sử dụng tập dữ liệu sau –

1.0, 2.0, 0
3.0, 4.0, 0
5.0, 2.0, 0
6.0, 3.0, 0
8.0, 1.0, 0
9.0, 2.0, 0
1.0, 4.0, 1
2.0, 5.0, 1
4.0, 6.0, 1
6.0, 5.0, 1
7.0, 3.0, 1
8.0, 5.0, 1

Để bắt đầu triển khai mô hình LR này trong CNTK, trước tiên chúng ta cần nhập các gói sau – import numpy as npimport cntk as C

Chương trình được cấu trúc với hàm main() như sau:

def main():
print("Using CNTK version = " + str(C.__version__) + "\n")

Bây giờ, chúng ta cần tải dữ liệu huấn luyện vào bộ nhớ như sau –

data_file = ".\\dataLRmodel.txt"
print("Loading data from " + data_file + "\n")
features_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",", skiprows=0, usecols=[0,1])
labels_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",", skiprows=0, usecols=[2], ndmin=2)

Bây giờ, chúng tôi sẽ tạo một chương trình đào tạo tạo mô hình hồi quy logistic tương thích với dữ liệu đào tạo –

features_dim = 2
labels_dim = 1
X = C.ops.input_variable(features_dim, np.float32)
y = C.input_variable(labels_dim, np.float32)
W = C.parameter(shape=(features_dim, 1)) # trainable cntk.Parameter
b = C.parameter(shape=(labels_dim))
z = C.times(X, W) + b
p = 1.0 / (1.0 + C.exp(-z))
model = p

Bây giờ, chúng ta cần tạo Lerner và trainer như sau:

features_dim = 2
labels_dim = 1
X = C.ops.input_variable(features_dim, np.float32)
y = C.input_variable(labels_dim, np.float32)
W = C.parameter(shape=(features_dim, 1)) # trainable cntk.Parameter
b = C.parameter(shape=(labels_dim))
z = C.times(X, W) + b
p = 1.0 / (1.0 + C.exp(-z))
model = p

Bây giờ, chúng ta cần tạo Lerner và trainer như sau:

ce_error = C.binary_cross_entropy(model, y) # CE a bit more principled for LR
fixed_lr = 0.010
learner = C.sgd(model.parameters, fixed_lr)
trainer = C.Trainer(model, (ce_error), [learner])
max_iterations = 4000

Đào tạo mô hình LR

Khi chúng ta đã tạo mô hình LR, tiếp theo, đã đến lúc bắt đầu quá trình đào tạo –

np.random.seed(4)
N = len(features_mat)
for i in range(0, max_iterations):
row = np.random.choice(N,1) # pick a random row from training items
trainer.train_minibatch({ X: features_mat[row], y: labels_mat[row] })
if i % 1000 == 0 and i > 0:
mcee = trainer.previous_minibatch_loss_average
print(str(i) + " Cross-entropy error on curr item = %0.4f " % mcee)

Bây giờ, với sự trợ giúp của đoạn mã sau, chúng ta có thể in trọng số và độ lệch của mô hình –

np.set_printoptions(precision=4, suppress=True)
print("Model weights: ")
print(W.value)
print("Model bias:")
print(b.value)
print("")
if __name__ == "__main__":
main()

Huấn luyện mô hình hồi quy logistic – Ví dụ đầy đủ

import numpy as np
import cntk as C
   def main():
print("Using CNTK version = " + str(C.__version__) + "\n")
data_file = ".\\dataLRmodel.txt" # provide the name and the location of data file
print("Loading data from " + data_file + "\n")
features_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",", skiprows=0, usecols=[0,1])
labels_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",", skiprows=0, usecols=[2], ndmin=2)
features_dim = 2
labels_dim = 1
X = C.ops.input_variable(features_dim, np.float32)
y = C.input_variable(labels_dim, np.float32)
W = C.parameter(shape=(features_dim, 1)) # trainable cntk.Parameter
b = C.parameter(shape=(labels_dim))
z = C.times(X, W) + b
p = 1.0 / (1.0 + C.exp(-z))
model = p
ce_error = C.binary_cross_entropy(model, y) # CE a bit more principled for LR
fixed_lr = 0.010
learner = C.sgd(model.parameters, fixed_lr)
trainer = C.Trainer(model, (ce_error), [learner])
max_iterations = 4000
np.random.seed(4)
N = len(features_mat)
for i in range(0, max_iterations):
row = np.random.choice(N,1) # pick a random row from training items
trainer.train_minibatch({ X: features_mat[row], y: labels_mat[row] })
if i % 1000 == 0 and i > 0:
mcee = trainer.previous_minibatch_loss_average
print(str(i) + " Cross-entropy error on curr item = %0.4f " % mcee)
np.set_printoptions(precision=4, suppress=True)
print("Model weights: ")
print(W.value)
print("Model bias:")
print(b.value)
if __name__ == "__main__":
  main()

đầu ra

Using CNTK version = 2.71000 cross entropy error on curr item = 0.19412000 cross entropy error on curr item = 0.17463000 cross entropy error on curr item = 0.0563Model weights:[-0.2049] [0.9666]]Model bias:[-2.2846]

Dự đoán bằng Mô hình LR đã được đào tạo

Khi mô hình LR đã được đào tạo, chúng ta có thể sử dụng nó để dự đoán như sau – Trước hết, chương trình đánh giá của chúng tôi nhập gói numpy và tải dữ liệu huấn luyện vào ma trận tính năng và ma trận nhãn lớp theo cách tương tự như chương trình đào tạo mà chúng tôi triển khai ở trên

import numpy as np
def main():
data_file = ".\\dataLRmodel.txt" # provide the name and the location of data file
features_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",",
skiprows=0, usecols=(0,1))
labels_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",",
skiprows=0, usecols=[2], ndmin=2)

Tiếp theo, đã đến lúc đặt các giá trị của trọng số và độ lệch đã được xác định bởi chương trình đào tạo của chúng tôi

print("Setting weights and bias values \n")
weights = np.array([0.0925, 1.1722], dtype=np.float32)
bias = np.array([-4.5400], dtype=np.float32)
N = len(features_mat)
features_dim = 2

Tiếp theo, chương trình đánh giá của chúng tôi sẽ tính toán xác suất hồi quy logistic bằng cách xem qua từng mục đào tạo như sau –

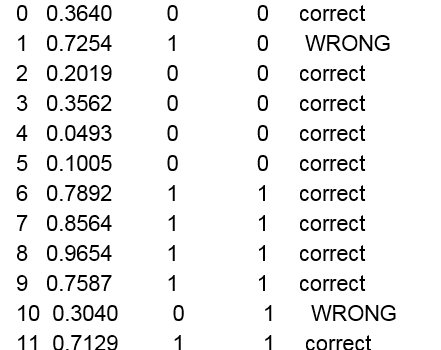
print("item pred_prob pred_label act_label result")
for i in range(0, N): # each item
   x = features_mat[i]
   z = 0.0
   for j in range(0, features_dim):
   z += x[j] * weights[j]
   z += bias[0]
   pred_prob = 1.0 / (1.0 + np.exp(-z))
  pred_label = 0 if pred_prob < 0.5 else 1
   act_label = labels_mat[i]

   pred_str = ‘correct’ if np.absolute(pred_label - act_label) < 1.0e-5 \
    else ‘WRONG’
  print("%2d %0.4f %0.0f %0.0f %s" % \ (i, pred_prob, pred_label, act_label, pred_str))

Bây giờ chúng ta hãy trình bày cách thực hiện dự đoán –

x = np.array([9.5, 4.5], dtype=np.float32)
print("\nPredicting class for age, education = ")
print(x)
z = 0.0
for j in range(0, features_dim):
z += x[j] * weights[j]
z += bias[0]
p = 1.0 / (1.0 + np.exp(-z))
print("Predicted p = " + str(p))
if p < 0.5: print("Predicted class = 0")
else: print("Predicted class = 1")

Hoàn thành chương trình đánh giá dự đoán

import numpy as np
def main():
data_file = ".\\dataLRmodel.txt" # provide the name and the location of data file
features_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",",
skiprows=0, usecols=(0,1))
labels_mat = np.loadtxt(data_file, dtype=np.float32, delimiter=",",
skiprows=0, usecols=[2], ndmin=2)
print("Setting weights and bias values \n")
weights = np.array([0.0925, 1.1722], dtype=np.float32)
bias = np.array([-4.5400], dtype=np.float32)
N = len(features_mat)
features_dim = 2
print("item pred_prob pred_label act_label result")
for i in range(0, N): # each item
   x = features_mat[i]
   z = 0.0
   for j in range(0, features_dim):
     z += x[j] * weights[j]
   z += bias[0]
   pred_prob = 1.0 / (1.0 + np.exp(-z))
   pred_label = 0 if pred_prob < 0.5 else 1
   act_label = labels_mat[i]
   pred_str = ‘correct’ if np.absolute(pred_label - act_label) < 1.0e-5 \
     else ‘WRONG’
  print("%2d %0.4f %0.0f %0.0f %s" % \ (i, pred_prob, pred_label, act_label, pred_str))
x = np.array([9.5, 4.5], dtype=np.float32)
print("\nPredicting class for age, education = ")
print(x)
z = 0.0
for j in range(0, features_dim):
   z += x[j] * weights[j]
z += bias[0]
p = 1.0 / (1.0 + np.exp(-z))
print("Predicted p = " + str(p))
if p < 0.5: print("Predicted class = 0")
else: print("Predicted class = 1")
if __name__ == "__main__":
  main()